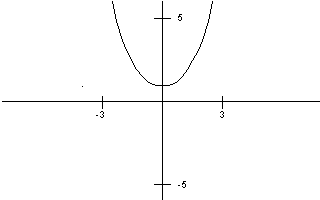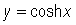 is defined in terms of the exponential function as follows
is defined in terms of the exponential function as followsGraphing y = Cosh x
We know that 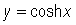 is defined in terms of the exponential function as follows
is defined in terms of the exponential function as follows
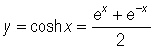
By rewriting the function as
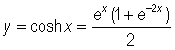
and noting that both factors in the numerator, as well as the denominator are positive for all values of x, we have that the graph of 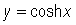 is always positive (in fact, it is always > = 1).
is always positive (in fact, it is always > = 1).
Now, the first derivative of 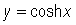 is given by
is given by
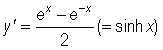
which may rewritten as
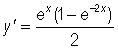
If x < 0, (the second factor in the numerator) 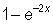 < 0 ; and if x > 0, the expression
< 0 ; and if x > 0, the expression 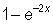 > 0.
> 0.
So, since 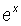 is always positive, and the denominator (= 2) of
is always positive, and the denominator (= 2) of 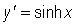 is always positive, we have that
is always positive, we have that

So, the graph of the function 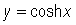 is decreasing when x < 0 and increasing when x > 0.
is decreasing when x < 0 and increasing when x > 0.
Now, we take the second derivative of 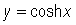 and obtain
and obtain
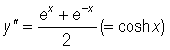
we have already noted that 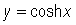 is positive for all values of x, so the graph is always concave up.
is positive for all values of x, so the graph is always concave up.
Below is the graph of 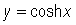 .
.