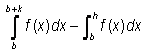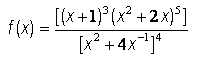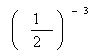|
CALCULUS II
|
REVIEW FOR FINAL EXAM
|
SPRING 2003
|
1. a. Rank the approximating rules Upper or Lower Rectangles, Trapezoid, and Simpson in order of their accuracy in estimating error under polynomial curves. Explain your answer as fully as you can.
b. As the power of a function increases, what happens to the error and percentage error using the Trapezoid and Simpson’s rule?
a. Explain the answer in part b. above.
2. Find the error estimate for the function y = 6x2 - 20x5, on [0,4], for n = 10, using the
Simpson's rule estimate, 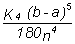 , and the Trapezoid rule estimate,
, and the Trapezoid rule estimate, 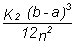 , where
, where
K4 and K2 represent, 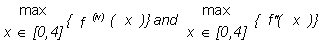 respectively in the formulas above.
respectively in the formulas above.
3. Using the limit of Riemann sums, find the area under the curve y = 3x2 - 5x + 13on [0,5].
4. a. 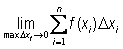 = under on [a, b] when f (x) .
= under on [a, b] when f (x) .
b. If f(x) < 0 on [a, b],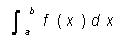 is , because .
is , because .
c. If f(x) is above and below the x–axis on [a, b], then 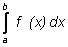 . Illustrate your answers.
. Illustrate your answers.
5. Solve the differential equation f ² (x) = 3x2 - 3, f ¢ (1) = 1, f (-1) = 3.
6. Find the average value of f (x) = x3 + 2x2 + 3 on [0, 3].
7. Express 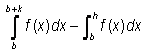 as one integral.
as one integral.
8. Find the area of the regions between the graphs of f (x) = 3 - x2 and g (x) = -1 on the interval [-4,2].
9. Evaluate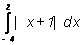 .
.
10. Find the volume generated by revolving the region between y =  , y = 0, x = 1 and x = 5 about x = 6.
, y = 0, x = 1 and x = 5 about x = 6.
11. Find the area of the surface obtained by revolving the curve  about the x-axis on the interval [0,3].
about the x-axis on the interval [0,3].
12. Find f -1 (x) for f (x) = 3 + 5x2, x <= 0, and sketch the graph of f (x) and f -1 (x) below. State the domain and range of the function and its inverse.
13. Use logarithmic differentiation to find f ’(x)  for
for 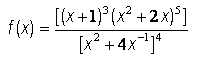
14. a. State the integral definition of y = ln x; and show (graphically) why it makes sense.
b. State the Fundamental Theorem of Calculus (this shows how to differentiate an integral).
c. Apply the above theorem to differentiate y = ln x.
15. Find the center of mass of the region between y = x5 and y = x7 on the interval [0,1].
16. Find f ¢(x) for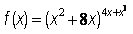 .
.
17. When you bring a 150° sheet of metal into a 55° room, the temperature of the plate is 120° after 15 minutes. How long will it take for the plate to cool to 70°?
(Hint: 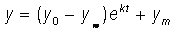 .)
.)
18. Derive the logarithmic form for y = tan h -1 x or sin h -1 x find its derivative and write the corresponding integral form.
19. Derive the exponential growth (decay) law starting with 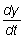 µ y.
µ y.
20. Derive the derivative of the function y = ex.
21. Find f ¢(x) for f (x) =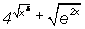 .
.
22. The equation y = 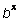 may be written as =
may be written as = 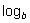 . Since 34 = , we may also write
. Since 34 = , we may also write 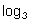 = and since
= and since 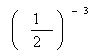 = , we may also write
= , we may also write 
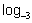 = .
= .
23. Derive the derivative of y = tan-1 x and write the corresponding integral form.
![]() , and the Trapezoid rule estimate,
, and the Trapezoid rule estimate, ![]() , where
, where![]() respectively in the formulas above.
respectively in the formulas above.