Proving that 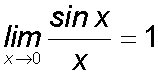
Proving that 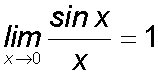
We will use the picture above to prove that 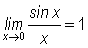 .
.
First, we note that

Since the area of a triangle is given by the formula 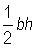 and the area of a circular sector is given
and the area of a circular sector is given 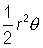 , the above inequality becomes
, the above inequality becomes
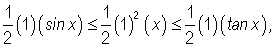
as the base of both triangles, as well as the radius of the circle are "1", and the height of the triangles are, respectively,
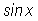 and
and 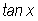 .
.
Now, we multiply the inequality above by
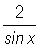
to obtain the new inequality
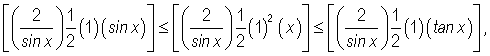
which simplifies to
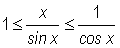
Now, we take the reciprocal of each term in the inequality (which reverses the direction of the inequality) and rearrange the terms in increasing order, to obtain
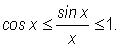
We obtain the desired result upon noting that the first and last term
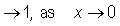
and so the term
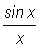
also has, by applying the Squeeze Theorem, a limit of 1.