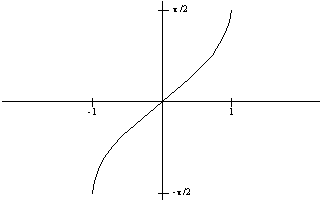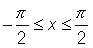the graph of 
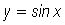is always increasing. This is most easily verified by noting the derivative of 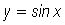is 
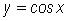and that on the interval 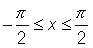(i.e. quadrants I and IV) we have that 
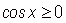.Graphing Sin -1 x
On the interval,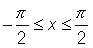 the graph of 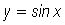is always increasing. This is most easily verified by noting the derivative of 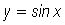is 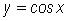and that on the interval 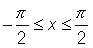(i.e. quadrants I and IV) we have that .
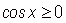When a function is always increasing (or decreasing) - this property is called monotonic - it will have an inverse. So, we will find the inverse of 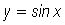on the interval .
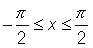The graph of 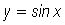on the interval 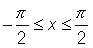looks like:
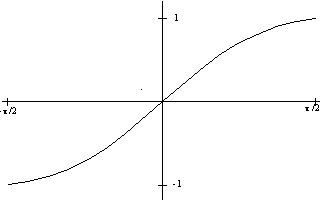
When a function has an inverse, we can find this inverse by transitioning the graph through two rotations.
First, we rotate the graph and the axes counter-clockwise about the origin 90 degrees -- so, the y-axis becomes the x-axis and vice-versa. This changes the above graph as below:
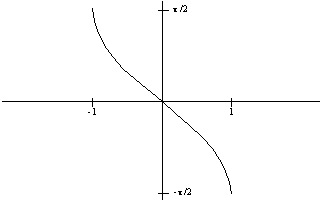
Next, we keep the y-axis in the same position as above, but rotate the graph (and the x-axis) 180 degrees about the y-axis. This changes the above graph into the inverse of the original function:
