Proofs and Derivations
The Derivative of the Inverse of cosh x

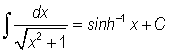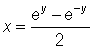
The Derivative of Sinh -1 x
 

Let y = sinh -1 x
 

We have no rules that will allow us to differentiate this function, so we are going to first write it into another form, so that we can apply differentiation rules that we have developed.

Apply the function sinh x to both sides of this equation, to obtain
 
 
 

sinh y = x


 

Rewrite this as,
 
 

x = sinh y



 

Now, we may rewrite the above function--using the exponential form of the hyperbolic sine function--as,
 
 


 

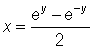
Multiply both sides of this equation by '2' and then flip the equation to obtain
 
 
 



 

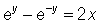
Now, multiply both sides of this equation by 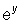, so the equation becomes
 
 
 



 

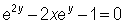
and this may rewritten as
 
 

.
 
 

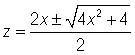Now, we may seem to have created a mess, but we will soon be able to solve this equation for y and obtain a form that we can differentiate.

We now let  z = 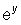, so that the above equation turns into a quadratic equation in z
 
 
 

z2 - 2xz - 1 = 0.



 

We can solve this equation for z (using   ?   method) and obtain
 
 
 


 

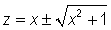
which simplifies to
 
 

.



 

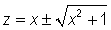Now, since z = 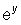(and  is always   ?  than 0), we may rewrite this as
 
 
 



 

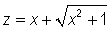
(or the left side of this equation would be negative).

Now replace z with 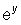 and rewrite the above equation as
 
 
 



 

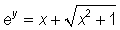
and the natural logarithmic function (ln x) to both sides of this equation to obtain,
 
 
 

.
 
 

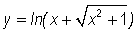We have now achieved our first goal of rewriting the function y = sinh -1x in a form which can be differentiated.

So, let's differentiate the above equation. We get
 
 
 


 

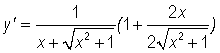
which simplifies to
 
 



 

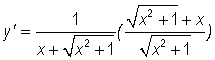
and further simplifies to
 
 

.



 

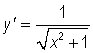We have now completed this derivation, as we now know that
 
 
 



 

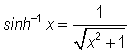
which has the integral form