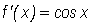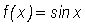
![]()
Deriving the Derivative of Sin x
We let
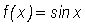
![]()
and take the formal derivative of 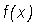
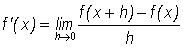
Next, we apply the above definition to our function, 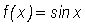 , to obtain
, to obtain
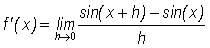 .
.
Now, we expand the expression 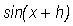 as follows
as follows
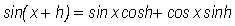
so, we then have that our derivative of 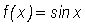 is
is
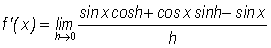 .
.
To resolve this limit we cleverly rearrange the terms in the numerator as follows
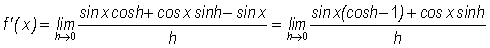
so that we may split the limit into the two parts
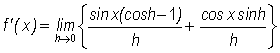 .
.
Upon rearranging further to
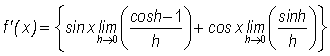 ,
,
we may then take the above limits to obtain
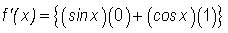
which gives us our result