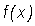be continuous on the interval 
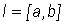and let 
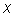be a point of 
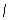. Then if 
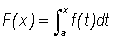, we have
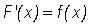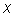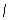at each point in .The Second Fundamental Theorem of Calculus
Let 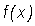be continuous on the interval 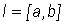and let 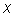be a point of 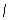. Then if 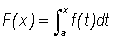, we have 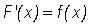at each point 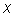in .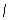
Proof:
We know from Calculus I, that
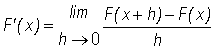(1)
Since 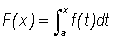, each expression in the numerator of (1) is an integral, and so we rewrite (1) as
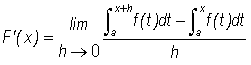(2)
Because of the Addition Rule for integrals we can combine the two integrals in the numerator above and rewrite the equation as
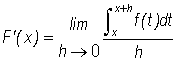(3)
Now, let's note an important property, the Rectangle Property for integrals.
o Let f be a continuous function on an interval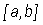 
. If 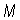and 
and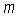 
are, respectively, the maximum and minimum values of 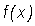on 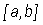, then
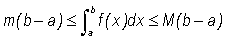
Using this property we note that
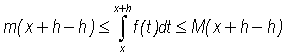(4)
or that
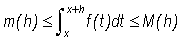(5)
and so using (5) we may rewrite expression (3) as
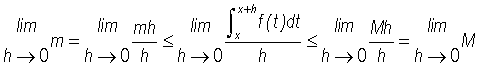(6)
o Note that: As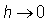 
above, the interval 
degenerates to a single point, .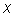
And so, as 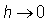, both 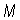and 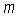, the maximum and minimum values of 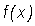respectively, are the maximum and minimum values of 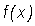on an interval with only the point, 
.
As both of these must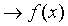 
, the theorem is proven.