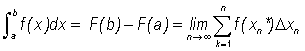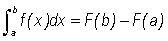 (1)
(1)
The First Fundamental Theorem of Calculus
If f(x) is continuous on [a, b] and if F is the antiderivative of f on [a, b], then
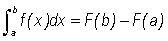 (1)
(1)
Proof:
Let the points 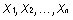 be a partition of (randomly chosen points in) the interval [a, b] such that
be a partition of (randomly chosen points in) the interval [a, b] such that
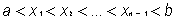 .
.
These points divide [a, b] into n subintervals
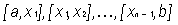 (2)
(2)
whose lengths we will denote as
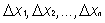 (3)
(3)
Now, we write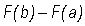 as a telescoping sum:
as a telescoping sum:
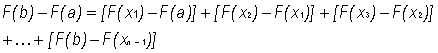 (4)
(4)
Since F is continuous and differentiable on [a,b], it satisfies the hypotheses of the Mean Value Theorem on each subinterval in (2).
Hence, each of the terms
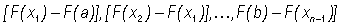
on the right side of equation (4) can be rewritten using this theorem, and so equation (4) becomes
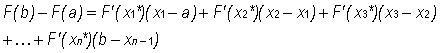 (5)
(5)
where the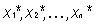 are (as required by the theorem) arbitrary points in their respective subinterval of line (2).
are (as required by the theorem) arbitrary points in their respective subinterval of line (2).
By hypothesis,
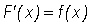 (6)
(6)
for all x in [a, b]. So, using (3) and (6) we can rewrite (5) as
![]()
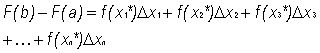
or in sigma notation,
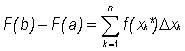 (7)
(7)
We note that the above relationship holds for all n, and so it holds as 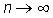 .
.
Now, we let the upper limit, n, of the sum on the right side of (7) approach infinity so that the maximum width of the subintervals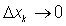 .
.
In module 14 we learned that the limit of the sum on the right side of (7) as 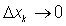 is
is
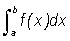
Having proved the equivalence of the three expressions below, we have proven the theorem.